統計検定2級に合格しました!
合格体験記はこちらの記事で紹介しています。
https://liberal.triplearner.com/2022/03/05/statistical/
この記事では、勉強しながら作ったチートシートを公開しています。
正規分布とは?検定とは?という理解が必要な話は置いておいて、試験前に暗記する必要があった内容です。
諸々の用語
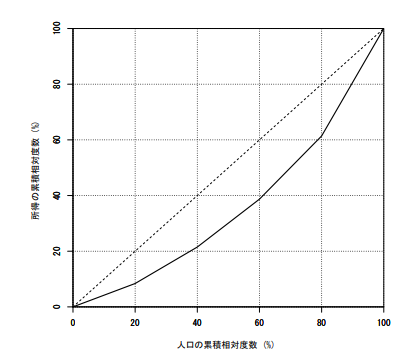
ローレンツ曲線
完全平等線と実線の間の面積の2倍がジニ係数
尖度と歪度
歪度:右裾が長いときに正、左裾が長いときに負
尖度:正規分布よりとがっているときに正、平たいときに負
変動係数
標準偏差を平均値で割った数
事象
排反事象:同時には起きない
独立:\(P(A)+P(B)-P(A\cap B)=P(A\cup B)\)
フィッシャーの三原則
- 無作為化:制御できない要因の影響を偶然誤差に転化する
- 繰り返し:複数の処理を比較する時に、同じ条件で2回以上繰り返し実験する。
同じ条件を複数の被験者で試す - 局所管理:実験を行う時間や場所を区切ってブロックを作り、ブロック内の条件をできるだけ同じにする
価格指数
- ラスパイレス指数:基準年の数量を重みとする
\[ \frac{比較年の価格×基準年の数量}{基準年の価格×基準年の数量} \] - パーシェ指数:比較年の数量を重みとする
\[\frac{比較年の価格×比較年の数量}{基準年の価格×比較年の数量}\]
中心極限定理
抽出するサンプルサイズが大きくなるにつれて、標本平均は正規分布\(N(μ,\frac{σ^2}{n})\)に近づく
推定量
- 不偏推定量
サンプルサイズに関係なく期待値が母数と一致する性質。 - 一致推定量
サンプルサイズを大きくすれば母平均に近づく性質。一致推定量でも不偏推定量とは限らない。
標準誤差
標本から得られる推定量のばらつき。不偏分散で計算する。
\[ SE=\frac{s} {\sqrt{n}} \]
標本の抽出方法
- 層化抽出法
母集団をいくつかのグループに分けて、各グループから必要な数の調査対象を無作為に抽出 - 層化二段抽出法
層化抽出されたグループの中から、無作為抽出をする - 二層抽出法
層化抽出は各グループで必要な調査対象数が分かっていないとできないので、まず母集団から標本を抽出して母集団の情報を取得してから層化抽出を行う - 集落抽出法(クラスター抽出法)
母集団を小集団に分け、分けられた小集団の中から無作為抽出する。それぞれの小集団で全数調査を行う - 多段抽出法
母集団をグループに分け、さらにその中でグループを選び、、最終的なグループの中から調査対象を無作為抽出 - 系統抽出法
通し番号を付けて、1番から等間隔に調査対象を選ぶ
期待値と分散の公式
\(E[aX] = aE[X]\)
\(E[X+a] = E[X]+a\)
\(V[aX] = a^2V[X]\)
\(V[X+a] = V[X]\)
\(V[X] = E[X^2]-E[X]^2\)
\(Cov(X,Y)=E[XY]-E[X]E[Y]\)
\(V(X+Y)=V(X)+V(Y)+2Cov(X,Y)\)
\(V(X-Y)=V(X)+V(Y)-2Cov(X,Y)\)
\(Cov(X,Y)\)は共分散で、XとYが独立なら0になる。共分散の最大値は1ではない。
\(Cov(X,X)=V(X)\)
標本の分散は不偏分散で考える。
\(不偏分散=\frac{n}{n-1}\sigma^2\)
相関係数
\[r_{xy}=\frac{\frac{1}{n} \sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sqrt{\frac{1}{n}\sum_{i=1}^{n} (x_{i}-\bar{x})^2}\times \sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_{i}-\bar{y})^2}} = \frac{Cov(X,Y)}{\sqrt{V(X)V(V)}}\]
x,yに定数を足したり引いたりしても共分散、相関係数は変わらないが、x,yのどちらか一方でも2倍にすれば、共分散は2倍になる
偏相関係数は、第3の因子の影響を除いた相関係数
分布
二項分布
表と裏のように二通りしかない試行がベルヌーイ試行で、複数回行ったベルヌーイ試行の成功回数が従う分布が二項分布。
\[E(X)=np\]
\[V(x)=np(1-p)\]
ポアソン分布
二項分布のnが十分大きくpが十分小さければ、ポアソン分布に従う。
\[E(X)=V(X)=np\]
幾何分布
成功確率が\(p\)の時、初めて成功するまでの試行回数が従う分布。
\[E(X)=\frac{1}{p}\]
\[V(X)=\frac{1-p}{p^2}\]
正規分布
平均や標準偏差が異なる値も、以下の公式に当てはめて正規化すればN(0,1)の正規分布として比較できる
\[z=\frac{X-μ}{σ}\]
確率関数
確率質量関数
さいころのように、事象の数が決まっている変数が離散変数で、確率質量関数に従う。Nは事象の数。
\[E(X)=\frac{N+1}{2}\]
\[V(X)=\frac{N^2-1}{12}\]
確率密度関数
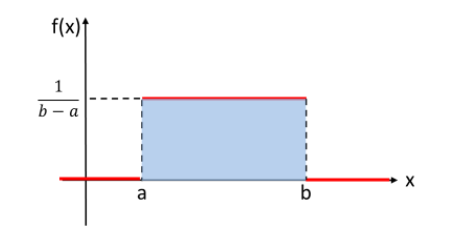
体重のように、連続した値をとる変数が連続型変数で、確率密度関数に従う。確率密度関数の上限は1ではないが、面積(確率の合計)は1になる。
取りうる値の期待値
\[E(X)=\frac{a+b}{2}\]
\[V(X)=\frac{(b-a)^2}{12}\]
値の期待値
\[E(X) = \int_{-\infty}^{\infty} xf(x)dx\]
累積分布関数
確率密度関数を積分すると累積分布関数になる。
上のグラフの累積分布関数なら
検定
- 第一の過誤:有意水準。帰無仮説が正しいのに、棄却域に入る確率
- 第二の過誤:対立仮設が正しいときに、棄却域に入らない確率
区間推定
母分散が分かる場合の母平均
\[\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}\]
母分散が分からない場合の母平均
自由度\((n-1)\)のt分布
\[t=\frac{\bar{x}-μ}{\sqrt{\frac{s^2}{n}}}\]
差の区間推定
\(s^2\)はプールした分散を使う。t分布の自由度は\(n_{1}+n_{2}-2\)
\[s^2_{p}=\frac{(n_{1}-1)s^2_{1}+(n_{2}-1)s^2_{2}}{n_{1}+n_{2}-2}\]
\[ t= \frac{\bar{x}_{1} - \bar{x}_{2}} {\sqrt{s^2_{p}(\frac{1}{n_{1}}+\frac{1}{n_{2}})}} \]
母比率
Zが正規分布の信頼区間内に入る
\[Z=\frac{\hat{p}-p}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}\]
差の区間推定
\(\hat{p}\)はプールした標本比率を使う。
\[\hat{p}=\frac{n_{1}\hat{p}_{1} + n_{2}\hat{p}_{2}} {n_{1}+n_{2}}\]
\[ z= \frac{\hat{p}_{1} - \hat{p}_{2}} {\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_{1}} + \frac{1}{n_{2}})}}\]
母分散
\(χ^2\)が自由度n-1のカイ二乗分布の信頼区間内に入る。カイ二乗分布は左右対称ではない。
\[χ^2 = \frac{(n-1)s^2}{σ^2}\]
独立性・適合度の検定
\[χ^2 = \frac{(実測値-理論値)^2}{理論値} +\ldots\]
カイ二乗分布の自由度は(横軸の数-1)×(縦軸の数-1)
片側検定
分散分析
F分布は、自由度が\(k_{1},k_{2}\)のカイ二乗分布の比で表すことができる。\(σ^2_{1}=σ^2_{2}\)と仮定すると不偏分散の比になるので、2つのサンプル群の母分散が等しいかどうかを検定できる。
大きい方の不偏分散を分子にする。F分布の自由度は(大きい方のサンプル数-1,小さい方のサンプル数-1)
\[F=\frac{χ^2_{1}/k_{1}}{χ^2_{2}/k_{2}}=\frac{s^2_{1}/σ^2_{1}}{s^2_{2}/σ^2_{2}}\]
一元配置分散分析
| 因子 | 平方和 | 自由度 | 平均平方 | F値 |
| 水準間 | データ全体の平均-各水準の平均(因子の数分足す) | 水準の数-1 | 平方和/自由度 | 水準の平均平方/残渣の平均平方 |
| 残渣 | 各水準の平均-因子 | 差分 | 平方和/自由度 | |
| 全体 | データ全体の平均-因子 =要因の平方和+残渣の平方和 | データ全数-1 |
F分布の自由度は、(水準の自由度,残渣の自由度)
片側検定。帰無仮説は、各郡の母平均は全て等しい。
回帰分析
nはサンプルの数、kは説明変数の数。
\(\hat{\beta}_{i}\)は偏回帰係数(estimate)
\[残渣の標準誤差^2 = \frac{残渣平方和}{(n-k-1)}\]
決定係数(Multiple R-squared):
単回帰式の当てはまりの良さを表す。説明変数が増えると大きくなるので、重回帰では使えない。
自由度調整済み決定係数(Adjusted R-squared):
説明変数の数を調整した決定係数。重回帰式の当てはまりの良さ。
偏回帰係数の有意性:
自由度n-k-1のt分布を使う。偏回帰係数が0ではないことを調べるなら以下の式。
\[t_{i} = \frac{\hat{\beta}_{i}-0}{se(\hat{\beta}_{i})}\]