今回も8点台のAssignment Activityがちらほら
数学なのに参考文献不足で減点ってどういうことよ?と思うものもありましたが、分数表記ではなく小数点表記にするなどは日本の学校的感覚を持って気を付けていれば減点回避できたなと思うものもありました。
内容は統計検定でやったことあるものが多かったです
Rの勉強ができると思っていたのですが、それは含まれてなかった。シラバスにはRをやるとは書いてないけどネットで調べるとRもやったと書いてあったので、最近内容が変わったんでしょうか?
だったらSophiaで取ることにしても良かったなと思いました
まあ、最近仕事でも統計予測の提案をしていたので、仕事にも活きるという意味では良かったかもしれない
Final Exam前の復習用にも学んだことをまとめていきます
Contents
サンプルの作り方
| サンプリング方法 | 説明 | 方法の例 | メリット | デメリット |
| Systematic Sampling | 一定の間隔で対象を選ぶ方法 | 顧客名簿に番号をふり、最初の1人をランダムに選び、その後は5人おきに選ぶ | 簡単・ランダム性あり | パターンが母集団に影響する場合、偏りが出ることがある |
| Cluster Sampling | 母集団をグループに分け、いくつかのグループを全体ごと選ぶ | 市内の10校のうち、ランダムに3校を選び、その学校の全生徒を調査 | コスト削減・実地調査に適している | クラスター内が母集団と似ていないと偏りが出る |
| Stratified Sampling | 母集団を層(strata)に分け、各層からランダムにサンプルを抽出 | 学生を学年別に分け、各学年から成績上位10人をランダムに選ぶ | 各層の特性を反映しやすく、精度が高い | 分類の手間・層の情報が必要 |
| Convenience Sampling | 手に入りやすい対象を選ぶ方法(非確率抽出) | 近くにいる友人や通行人にアンケートを取る | 簡単・早い | 偏りが強く、結果が母集団を代表しないことが多い |
| 尺度の種類 | 特徴 | 例 |
| Nominal | データは分類のみ。順序や間隔に意味はない | 性別(男・女・ノンバイナリー)、血液型、国名 |
| Ordinal | データに順序はあるが、間隔は不明確 | 満足度(高・中・低)、成績(A・B・C) |
| Interval | 順序があり、間隔も一定だが、絶対的なゼロがない | 気温(0度は気温がないわけではない)、IQスコア |
| Ratio | 間隔が一定で、絶対ゼロあり。最も情報量が多い | 体重、身長、年齢、収入、所要時間 |
値の分析方法
Stem and Leaf: 5432なら543がstem、2がleaf
四分位数:第3四分位数なら中央値を含めない後半の中央値
Percentile: 50th percentileが中央値と同じ
standard deviation: 標準偏差。分散の平方根

外れ値の検出
- IQR
- IQR=Q3-Q1
- Q3+1.5×IQR以上、または、Q1-1.5×IQR以下が外れ値
- Z-score
- \[z=\frac{X-μ}{σ}\]
- Z-scoreが3以上、または、-3以下の場合、平均より3標準偏差分違うので外れ値
確率
| 用語 | 説明 |
| Experiment | 実験とは、管理された条件下で計画的に行われる操作。 結果が予測できない場合は「偶然性のある実験」。例:コインを2回投げる。 |
| Outcome | 実験の1回ごとの結果。例:コインを投げて「表(Heads)」が出ること。 |
| Sample Space (S) | 実験のすべての可能なOutcomeの集合。例:コイン1回投げる場合 S = {H, T}。 |
| Event | Outcomeの任意の組み合わせ。大文字(A, Bなど)で表す。例:1回のコイン投げで「表が1回以内」。 |
| Probability | イベントが起こる確からしさ。値は0~1の間。例:P(A) = 0 は「絶対起こらない」、P(A) = 1 は「必ず起こる」。 |
| Equally Likely | すべての結果が同じ確率で起こる場合。例:公平なサイコロは1~6が等確率で出る。 |
| Law of Large Numbers | 実験を多数回繰り返すと、相対頻度が理論的な確率に近づく。短期では偏りがあっても、長期には安定する。 |
| Biased vs. Fair | 結果が等確率でなければ「偏りあり(biased)」。例:あるユーロ硬貨で表が56%、裏が44% → 偏りの可能性あり。 |
Discrete Random Variable: 離散変数
数えられる変数のことで、身長やスピードなどは数えられないので当てはまらない
Binomial Distribution: 二項分布
成功と失敗という2つの結果しかないベルヌーイ試行で使う
nを大きくしてpを0.5に近づけると正規分布になる
\[E(X)=np\]
\[V(x)=np(1-p)\]
Poisson Distribution: ポアソン分布
二項分布のnが大きくpが小さいときに使う。その時間に発生する確率は分からなくても全体での発生確率が分かるなどのレアな事象を観察するのに適している。
λは平均であり分散。
λが小さいときは左に傾き、大きいときは分散も大きいので左右対称な状態
\[E(X)=V(X)=np\]
\[f(x)=\frac{e^{-λ}λ^x}{x!}\]
Geometric Distribution: 幾何分布
ベルヌーイ試行を何回か繰り返すときに、初めて成功するまでの回数を確率変数X、各試行の成功確率をpとしたときの確率分布
\[E(X)=\frac{1}{p}\]
\[V(X)=\frac{1-p}{p^2}\]
Hypergeometric Distribution: 超幾何分布
N個からなる集団が2つの性質(M,M-N)をもっているとする。そこからn個取り出すときに、片方の性質を持つ個数が特定値になる確率を調べる時に使う
\[E(X)=n\frac{M}{N}\]
\[V(X)=n\frac{M(N-M)}{N^2}\frac{N-n}{N-1}\]
Continuous Random Variables: 連続確率変数
体重のように、連続した値をとる変数が連続型変数。確率は面積で考え、面積の合計は1になる。
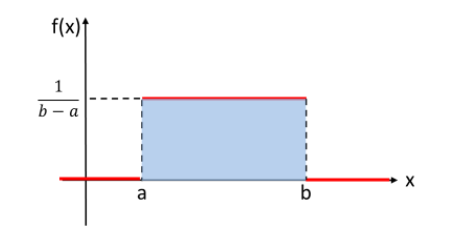
Uniform Distribution: 一様分布
一定範囲で確率が一定。全員5-15分の間で到着する時、7-10分の間で到着する確率なら(10-7)/(15-5)=0.3
\[E(X)=\frac{a+b}{2}\]
\[V(X)=\frac{(b-a)^2}{12}\]
Nominal Distribution: 正規分布
- シンメトリー
- Mean=Median=Mode
- Empirical rule
正規分布に従うデータにおいて、平均値から±1、2、3標準偏差の範囲内に、それぞれ約68%、95%、99.7%のデータが含まれる
Exponential Distribution: 指数分布
次に何かが起こるまでの期間を調べる時に使う
\[E(X)=\frac{1}{λ}\]
\[V(X)=\frac{1}{λ^2}\]
Cumulative Distribution: 累積分布関数
確率密度関数を積分(integral)すると累積分布関数になる。
ある期間に平均λ回起こる現象が次に起きるまでの期間をXとしたとき、期間Xがx以下になる確率は
\[F(x)=1-e^-λx\]
Central Limit Theorem: 中心極限定理
nが大きいとき、元の分布がどうなっていようと平均との差は正規分布になる
\[σx=\frac{σ}{\sqrt{n}}\]
感想
統計検定2級を受けていたので、新しい内容はないのですが、こうやって強制されないと復習することもないのでその点では良かったなと
UoPeople全体がそんな感想です。別に大学という形でなくても学べるけど、お金払ってコースとして体系化してくれないと自分からはやらないからなー、と。
結果はA+を逃してA
初めてのRequired Proctorコースでしたが、計算式を全部暗記しなくてもExcel使ってOKなので電卓だけで計算しないといけない統計検定より簡単です。勉強時間や緊張感という意味でも統計検定の方が大変だった。
何でこのコースだけProctor必須だったのか良く分からないですね